A Ladder 104 Meters Long Makes an Angle of 68 Degrees With the Ground as It Leans Again
Math Models
28 Solve Geometry Applications: Triangles, Rectangles, and the Pythagorean Theorem
Learning Objectives
By the end of this section, you will be able to:
- Solve applications using properties of triangles
- Use the Pythagorean Theorem
- Solve applications using rectangle properties
Solve Applications Using Properties of Triangles
In this department we volition use some common geometry formulas. Nosotros volition suit our problem-solving strategy so that we can solve geometry applications. The geometry formula volition name the variables and requite usa the equation to solve. In addition, since these applications will all involve shapes of some sort, about people find information technology helpful to draw a figure and label it with the given information. We will include this in the offset step of the problem solving strategy for geometry applications.
Solve Geometry Applications.
- Read the problem and brand certain all the words and ideas are understood. Draw the effigy and characterization it with the given information.
- Identify what we are looking for.
- Label what we are looking for by choosing a variable to represent information technology.
- Interpret into an equation past writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using skillful algebra techniques.
- Cheque the respond by substituting it back into the equation solved in pace five and by making certain it makes sense in the context of the problem.
- Respond the question with a consummate sentence.
We volition start geometry applications by looking at the properties of triangles. Let'southward review some basic facts about triangles. Triangles have three sides and three interior angles. Ordinarily each side is labeled with a lowercase letter of the alphabet to friction match the uppercase alphabetic character of the opposite vertex.
The plural of the discussion vertex is vertices. All triangles have three vertices. Triangles are named by their vertices: The triangle in (Figure) is called ![]()
Triangle ABC has vertices A, B, and C. The lengths of the sides are a, b, and c.

The three angles of a triangle are related in a special way. The sum of their measures is ![]() Note that we read
Note that we read ![]() every bit "the measure of bending A." So in
every bit "the measure of bending A." So in ![]() in (Effigy),
in (Effigy),
![]()
Because the perimeter of a figure is the length of its purlieus, the perimeter of ![]() is the sum of the lengths of its three sides.
is the sum of the lengths of its three sides.
![]()
To find the area of a triangle, we need to know its base of operations and height. The height is a line that connects the base to the contrary vertex and makes a ![]() angle with the base. We will draw
angle with the base. We will draw ![]() again, and at present show the height, h. See (Figure).
again, and at present show the height, h. See (Figure).
The formula for the area of ![]() is
is ![]() where b is the base and h is the summit.
where b is the base and h is the summit.
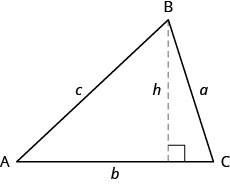
Triangle Properties
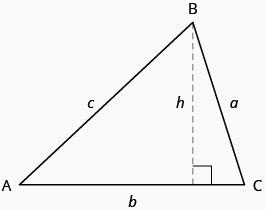
For ![]()
Angle measures:
![]()
- The sum of the measures of the angles of a triangle is
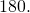
Perimeter:
![]()
- The perimeter is the sum of the lengths of the sides of the triangle.
Area:
![]()
- The area of a triangle is one-half the base of operations times the meridian.
The measures of ii angles of a triangle are 55 and 82 degrees. Find the measure of the third angle.
The measures of ii angles of a triangle are 31 and 128 degrees. Find the measure of the third angle.
21 degrees
The measures of ii angles of a triangle are 49 and 75 degrees. Detect the measure of the tertiary angle.
56 degrees
The perimeter of a triangular garden is 24 anxiety. The lengths of 2 sides are four feet and nine anxiety. How long is the third side?
The perimeter of a triangular garden is 48 anxiety. The lengths of 2 sides are 18 feet and 22 feet. How long is the third side?
8 feet
The lengths of two sides of a triangular window are vii feet and five anxiety. The perimeter is 18 feet. How long is the tertiary side?
half dozen feet
The area of a triangular church building window is 90 square meters. The base of the window is 15 meters. What is the window's summit?
The area of a triangular painting is 126 square inches. The base of operations is 18 inches. What is the height?
14 inches
A triangular tent door has area 15 foursquare anxiety. The tiptop is five anxiety. What is the base?
6 anxiety
The triangle properties we used so far utilise to all triangles. Now we will look at i specific type of triangle—a correct triangle. A right triangle has one ![]() angle, which we ordinarily mark with a modest square in the corner.
angle, which we ordinarily mark with a modest square in the corner.
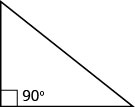
Correct Triangle
A right triangle has one ![]() angle, which is often marked with a square at the vertex.
angle, which is often marked with a square at the vertex.
I angle of a correct triangle measures ![]() What is the measure of the third angle?
What is the measure of the third angle?
One bending of a right triangle measures ![]() What is the measure of the other pocket-size angle?
What is the measure of the other pocket-size angle?
![]()
One angle of a right triangle measures ![]() What is the measure of the other small-scale angle?
What is the measure of the other small-scale angle?
![]()
In the examples nosotros accept seen so far, we could draw a figure and characterization it directly after reading the trouble. In the side by side example, we will take to ascertain one angle in terms of another. Nosotros will wait to draw the figure until we write expressions for all the angles nosotros are looking for.
The mensurate of one angle of a right triangle is 20 degrees more than than the measure of the smallest bending. Find the measures of all three angles.
The measure of one bending of a right triangle is fifty° more than than the measure of the smallest angle. Find the measures of all three angles.
![]()
The measure of one angle of a right triangle is 30° more than the measure of the smallest angle. Find the measures of all three angles.
![]()
Employ the Pythagorean Theorem
We accept learned how the measures of the angles of a triangle relate to each other. At present, we will learn how the lengths of the sides relate to each other. An of import property that describes the relationship among the lengths of the three sides of a right triangle is called the Pythagorean Theorem. This theorem has been used effectually the globe since ancient times. It is named after the Greek philosopher and mathematician, Pythagoras, who lived effectually 500 BC.
Before nosotros state the Pythagorean Theorem, we demand to introduce some terms for the sides of a triangle. Remember that a right triangle has a ![]() angle, marked with a small square in the corner. The side of the triangle contrary the
angle, marked with a small square in the corner. The side of the triangle contrary the ![]() angle is chosen the hypotenuse and each of the other sides are called legs.
angle is chosen the hypotenuse and each of the other sides are called legs.

The Pythagorean Theorem tells how the lengths of the three sides of a correct triangle relate to each other. It states that in any right triangle, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse. In symbols we say: in any right triangle, ![]() where
where ![]() are the lengths of the legs and
are the lengths of the legs and ![]() is the length of the hypotenuse.
is the length of the hypotenuse.
Writing the formula in every practise and saying it aloud as you write it, may help you remember the Pythagorean Theorem.
The Pythagorean Theorem
In whatever right triangle, ![]()
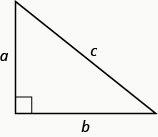
where a and b are the lengths of the legs, c is the length of the hypotenuse.
To solve exercises that utilize the Pythagorean Theorem, we will need to find foursquare roots. We accept used the notation ![]() and the definition:
and the definition:
If ![]() then
then ![]() for
for ![]()
For example, we found that ![]() is v because
is v because ![]()
Because the Pythagorean Theorem contains variables that are squared, to solve for the length of a side in a right triangle, nosotros volition have to utilize square roots.
Utilize the Pythagorean Theorem to find the length of the hypotenuse shown beneath.
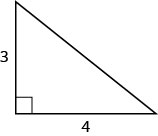
Employ the Pythagorean Theorem to find the length of the hypotenuse in the triangle shown below.
![]()
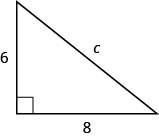
Use the Pythagorean Theorem to discover the length of the hypotenuse in the triangle shown below.
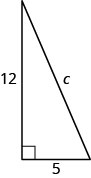
![]()
Use the Pythagorean Theorem to find the length of the leg shown below.
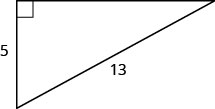
Apply the Pythagorean Theorem to observe the length of the leg in the triangle shown below.
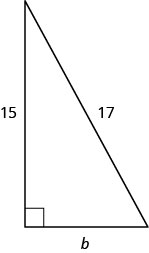
viii
Utilize the Pythagorean Theorem to find the length of the leg in the triangle shown below.
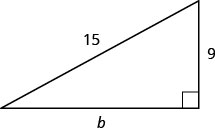
12
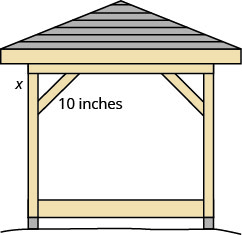
Kelvin is building a gazebo and wants to brace each corner by placing a ![]() slice of wood diagonally every bit shown above.
slice of wood diagonally every bit shown above.
If he fastens the forest so that the ends of the caryatid are the same distance from the corner, what is the length of the legs of the correct triangle formed? Gauge to the nearest 10th of an inch.
John puts the base of a 13-foot ladder five anxiety from the wall of his firm every bit shown below. How far up the wall does the ladder accomplish?

12 feet
Randy wants to attach a 17 foot string of lights to the superlative of the 15 foot mast of his sailboat, as shown below. How far from the base of the mast should he attach the cease of the lite string?
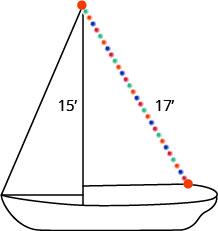
eight feet
Solve Applications Using Rectangle Properties
You lot may already be familiar with the properties of rectangles. Rectangles take four sides and 4 right ![]() angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, L, and its adjacent side equally the width, W.
angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, L, and its adjacent side equally the width, W.
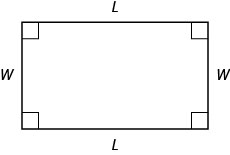
The distance around this rectangle is ![]() or
or ![]() This is the perimeter, P, of the rectangle.
This is the perimeter, P, of the rectangle.
![]()
What near the area of a rectangle? Imagine a rectangular rug that is 2-anxiety long past 3-feet wide. Its expanse is 6 square anxiety. In that location are six squares in the figure.
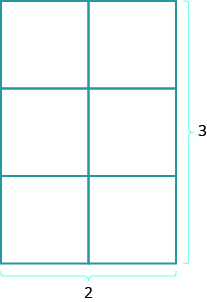
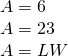
The area is the length times the width.
The formula for the area of a rectangle is ![]()
Properties of Rectangles
Rectangles have four sides and four correct ![]() angles.
angles.
The lengths of reverse sides are equal.
The perimeter of a rectangle is the sum of twice the length and twice the width.
![]()
The surface area of a rectangle is the product of the length and the width.
![]()
The length of a rectangle is 32 meters and the width is 20 meters. What is the perimeter?
The length of a rectangle is 120 yards and the width is 50 yards. What is the perimeter?
340 yards
The length of a rectangle is 62 anxiety and the width is 48 feet. What is the perimeter?
220 feet
The area of a rectangular room is 168 foursquare feet. The length is xiv feet. What is the width?
The area of a rectangle is 598 square feet. The length is 23 feet. What is the width?
26 feet
The width of a rectangle is 21 meters. The area is 609 square meters. What is the length?
29 meters
Detect the length of a rectangle with perimeter fifty inches and width ten inches.
Find the length of a rectangle with: perimeter eighty and width 25.
15
Discover the length of a rectangle with: perimeter thirty and width six.
9
We have solved issues where either the length or width was given, along with the perimeter or area; now we volition learn how to solve problems in which the width is divers in terms of the length. We volition expect to draw the figure until we write an expression for the width so that we tin label ane side with that expression.
The width of a rectangle is ii feet less than the length. The perimeter is 52 feet. Find the length and width.
The width of a rectangle is seven meters less than the length. The perimeter is 58 meters. Find the length and width.
18 meters, 11 meters
The length of a rectangle is eight anxiety more than than the width. The perimeter is lx feet. Find the length and width.
19 feet, xi feet
The length of a rectangle is iv centimeters more than twice the width. The perimeter is 32 centimeters. Find the length and width.
The length of a rectangle is eight more than than twice the width. The perimeter is 64. Discover the length and width.
24, 8
The width of a rectangle is half dozen less than twice the length. The perimeter is xviii. Find the length and width.
five, four
The perimeter of a rectangular swimming pool is 150 feet. The length is fifteen feet more than than the width. Detect the length and width.
The perimeter of a rectangular swimming pool is 200 feet. The length is 40 feet more than than the width. Discover the length and width.
lxx feet, 30 feet
The length of a rectangular garden is 30 yards more the width. The perimeter is 300 yards. Find the length and width.
90 yards, 60 yards
Key Concepts
- Problem-Solving Strategy for Geometry Applications
- Read the problem and make all the words and ideas are understood. Depict the figure and label it with the given information.
- Place what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the state of affairs. Substitute in the given data.
- Solve the equation using good algebra techniques.
- Check the answer in the trouble and make sure it makes sense.
- Answer the question with a complete sentence.
- Triangle Properties For
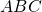
Bending measures:
Perimeter:
Area:
A right triangle has ane
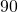 bending.
bending. -
- The Pythagorean Theorem In whatever right triangle,
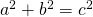 where c is the length of the hypotenuse and a and b are the lengths of the legs.
where c is the length of the hypotenuse and a and b are the lengths of the legs. - Properties of Rectangles
Practice Makes Perfect
Solving Applications Using Triangle Properties
In the following exercises, solve using triangle properties.
The measures of two angles of a triangle are 26 and 98 degrees. Find the mensurate of the third angle.
56 degrees
The measures of two angles of a triangle are 61 and 84 degrees. Find the measure out of the tertiary bending.
The measures of 2 angles of a triangle are 105 and 31 degrees. Notice the measure out of the 3rd bending.
44 degrees
The measures of ii angles of a triangle are 47 and 72 degrees. Discover the mensurate of the third angle.
The perimeter of a triangular pool is 36 yards. The lengths of 2 sides are 10 yards and fifteen yards. How long is the tertiary side?
11 feet
A triangular courtyard has perimeter 120 meters. The lengths of two sides are 30 meters and fifty meters. How long is the third side?
If a triangle has sides 6 feet and 9 feet and the perimeter is 23 feet, how long is the 3rd side?
8 feet
If a triangle has sides 14 centimeters and 18 centimeters and the perimeter is 49 centimeters, how long is the third side?
A triangular flag has base of operations ane human foot and height 1.5 foot. What is its area?
0.75 sq. ft.
A triangular window has base eight feet and height half dozen feet. What is its area?
What is the base of a triangle with surface area 207 square inches and height 18 inches?
23 inches
What is the height of a triangle with expanse 893 square inches and base 38 inches?
Ane angle of a right triangle measures 33 degrees. What is the measure of the other small angle?
57
Ane angle of a right triangle measures 51 degrees. What is the measure of the other modest angle?
One angle of a correct triangle measures 22.5 degrees. What is the mensurate of the other small angle?
67.5
I angle of a right triangle measures 36.five degrees. What is the measure of the other small bending?
The perimeter of a triangle is 39 feet. One side of the triangle is ane foot longer than the 2d side. The tertiary side is two anxiety longer than the second side. Detect the length of each side.
thirteen ft., 12 ft., xiv ft.
The perimeter of a triangle is 35 feet. 1 side of the triangle is five anxiety longer than the second side. The third side is 3 feet longer than the 2nd side. Find the length of each side.
One side of a triangle is twice the shortest side. The third side is 5 feet more than than the shortest side. The perimeter is 17 feet. Find the lengths of all three sides.
3 ft., 6 ft., 8 ft.
One side of a triangle is three times the shortest side. The third side is three feet more than the shortest side. The perimeter is 13 feet. Find the lengths of all three sides.
The two smaller angles of a right triangle accept equal measures. Find the measures of all three angles.
![]()
The measure of the smallest angle of a right triangle is 20° less than the measure of the next larger angle. Find the measures of all three angles.
The angles in a triangle are such that one angle is twice the smallest bending, while the 3rd bending is 3 times as large as the smallest angle. Detect the measures of all three angles.
![]()
The angles in a triangle are such that one bending is 20° more than the smallest bending, while the third angle is iii times equally large every bit the smallest angle. Find the measures of all 3 angles.
Utilize the Pythagorean Theorem
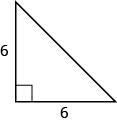
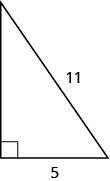
In the post-obit exercises, use the Pythagorean Theorem to find the length of the hypotenuse.
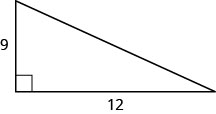
15
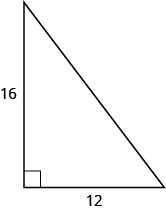
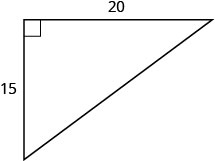
25
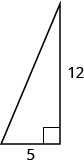
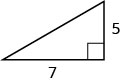
In the following exercises, use the Pythagorean Theorem to find the length of the leg. Circular to the nearest tenth, if necessary.
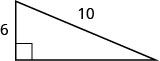
8
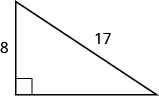
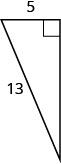
12
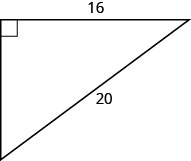
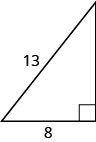
ten.2
9.8
In the following exercises, solve using the Pythagorean Theorem. Estimate to the nearest tenth, if necessary.
A 13-foot string of lights volition be fastened to the top of a 12-foot pole for a holiday display, as shown below. How far from the base of the pole should the end of the cord of lights be anchored?
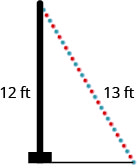
five feet
Pam wants to put a banner across her garage door, every bit shown beneath, to congratulate her son for his college graduation. The garage door is 12 anxiety loftier and 16 feet wide. How long should the imprint be to fit the garage door?

Chi is planning to put a path of paving stones through her flower garden, equally shown below. The flower garden is a foursquare with side 10 feet. What will the length of the path be?

14.1 anxiety
Brian borrowed a 20 foot extension ladder to apply when he paints his house. If he sets the base of operations of the ladder six feet from the house, equally shown beneath, how far up volition the top of the ladder reach?

Solve Applications Using Rectangle Properties
In the post-obit exercises, solve using rectangle properties.
The length of a rectangle is 85 feet and the width is 45 feet. What is the perimeter?
260 feet
The length of a rectangle is 26 inches and the width is 58 inches. What is the perimeter?
A rectangular room is 15 anxiety wide by 14 feet long. What is its perimeter?
58 anxiety
A driveway is in the shape of a rectangle 20 anxiety wide by 35 feet long. What is its perimeter?
The area of a rectangle is 414 square meters. The length is 18 meters. What is the width?
23 meters
The surface area of a rectangle is 782 square centimeters. The width is 17 centimeters. What is the length?
The width of a rectangular window is 24 inches. The area is 624 square inches. What is the length?
26 inches
The length of a rectangular poster is 28 inches. The surface area is 1316 square inches. What is the width?
Notice the length of a rectangle with perimeter 124 and width 38.
24
Discover the width of a rectangle with perimeter 92 and length 19.
Observe the width of a rectangle with perimeter 16.2 and length three.2.
four.nine
Detect the length of a rectangle with perimeter twenty.2 and width 7.8.
The length of a rectangle is nine inches more than the width. The perimeter is 46 inches. Find the length and the width.
16 in., 7 in.
The width of a rectangle is eight inches more than the length. The perimeter is 52 inches. Find the length and the width.
The perimeter of a rectangle is 58 meters. The width of the rectangle is five meters less than the length. Observe the length and the width of the rectangle.
17 m, 12 m
The perimeter of a rectangle is 62 feet. The width is 7 feet less than the length. Observe the length and the width.
The width of the rectangle is 0.7 meters less than the length. The perimeter of a rectangle is 52.6 meters. Find the dimensions of the rectangle.
13.5 grand length, 12.8 one thousand width
The length of the rectangle is 1.ane meters less than the width. The perimeter of a rectangle is 49.4 meters. Notice the dimensions of the rectangle.
The perimeter of a rectangle is 150 feet. The length of the rectangle is twice the width. Find the length and width of the rectangle.
50 ft., 25 ft.
The length of a rectangle is three times the width. The perimeter of the rectangle is 72 anxiety. Find the length and width of the rectangle.
The length of a rectangle is iii meters less than twice the width. The perimeter of the rectangle is 36 meters. Discover the dimensions of the rectangle.
7 chiliad width, 11 1000 length
The length of a rectangle is five inches more than than twice the width. The perimeter is 34 inches. Find the length and width.
The perimeter of a rectangular field is 560 yards. The length is twoscore yards more than the width. Discover the length and width of the field.
160 yd., 120 yd.
The perimeter of a rectangular atrium is 160 feet. The length is xvi feet more than than the width. Find the length and width of the atrium.
A rectangular parking lot has perimeter 250 feet. The length is five feet more than twice the width. Discover the length and width of the parking lot.
85 ft., twoscore ft.
A rectangular rug has perimeter 240 inches. The length is 12 inches more than twice the width. Detect the length and width of the carpeting.
Everyday Math
Christa wants to put a contend around her triangular flowerbed. The sides of the flowerbed are six feet, eight feet and 10 feet. How many feet of fencing will she need to enclose her flowerbed?
24 feet
Jose just removed the children's playset from his back yard to make room for a rectangular garden. He wants to put a fence around the garden to keep out the dog. He has a fifty foot roll of fence in his garage that he plans to employ. To fit in the backyard, the width of the garden must be x anxiety. How long can he brand the other length?
Writing Exercises
If you need to put tile on your kitchen floor, practise you demand to know the perimeter or the area of the kitchen? Explain your reasoning.
area; answers will vary
If you need to put a argue effectually your backyard, do you need to know the perimeter or the expanse of the backyard? Explain your reasoning.
Expect at the two figures beneath.

ⓐ Which figure looks similar it has the larger expanse?
ⓑ Which looks like it has the larger perimeter?
ⓒ Now calculate the area and perimeter of each figure.
ⓓ Which has the larger surface area?
ⓔ Which has the larger perimeter?
ⓐ Answers volition vary.
ⓑ Answers will vary.
ⓒ Answers will vary.
ⓓ The areas are the same.
ⓔ The 2×8 rectangle has a larger perimeter than the 4×4 square.
Write a geometry word problem that relates to your life experience, then solve it and explicate all your steps.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell y'all most your mastery of this section? What steps volition you take to improve?
Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-geometry-applications-triangles-rectangles-and-the-pythagorean-theorem/
0 Response to "A Ladder 104 Meters Long Makes an Angle of 68 Degrees With the Ground as It Leans Again"
Post a Comment